“Go for it マレーシア教育移住日記”のブログにご訪問いただきありがとうございます。
（今回の記事はちょっとマニアックですので、お嫌いな方はスルーしてください。）
日本人には耳慣れた概念である“偏差値”。
中学・高校・大学受験を控えた生徒さんや親御さんにとって、学力テストや定期テストで出される偏差値に一喜一憂することも多いのではないかと思います。
その偏差値ですが、実は海外で偏差値は存在しません。
なので、マレーシアに教育移住したお子さんが将来の大学進学を視野に入れた時、“希望する大学にはいったいどのくらいの偏差値が必要か？”という目安が掴めず、モヤモヤ感が募るものです。
今回の記事では、ド文系の道をひたすら歩んできたオジさんである僕が、難しい数式を一切抜きに、統計学の基本的なコンセプトの理解だけで、英国式A-Levelと国際バカロレア(IBDP)の“スコアと偏差値の対応関係”を提示し、さらにイギリスの名門大学に出願するために必要なスコア及びおおよその偏差値を出してみました。
ちなみに、偏差値算出には信頼できる名門大学の出願要件を参照元とし、僕個人の恣意的な要素は一切含んでおりません。
いつも応援クリックありがとうございます！
https://go-for-it-malaysia.com/the-first-year-of-alevel-at-epsom-college-in-malaysia/
統計学の基本的な知識だけでA-Levelと国際バカロレア(IBDP)の偏差値を出してみた (スコア＆偏差値対応表あり)
そもそも偏差値とは
偏差値は生データがないと算出できない
今は高1となった我が家の息子も、かつては中学受験に向けて小学校4年生からSAPIXに通い始め、毎月の学力テストの結果を受けて順位や偏差値に一喜一憂したものです。
一方で、海外では偏差値が存在しないので、《インターナショナルスクールに子供が入る場合の学校選びにおいて偏差値の基準はないのか？》とか、《大学進学に向けて、希望の大学の偏差値はどれくらいなのか？》など、偏差値がないことによって不安が募り、モヤモヤした気持ちになります。
そもそも“偏差値”とは高校数学で習う“確率分布”をベースとした概念ですが、高校で習う時点で難解な数式が出てくるため、文系脳の人は“数式アレルギー”を発症して理解不能となり、勉強する気が一気に萎えてしまうものです。
その確率分布を出すには、「生徒たちのテスト結果」という“生データ”が必要です。したがって、生データなしに偏差値も出すことはできません。
この前提に立ってみると、日本の各中学受験塾が公表している偏差値には少し違和感を覚えます。
なぜなら、受験生全体を母集団とする生データを持ってないのに、それぞれの塾が持つ内部データのみに基づいて各校の偏差値を出しているからです。
どういうことかというと、SAPIXの偏差値、日能研の偏差値、四谷大塚の偏差値がそれぞれ異なるという事態になっているのです。
例えば、名門・早稲田大学の直系附属中学である早稲田大学高等学院中学部の2023年偏差値は、SAPIXでは「56」であるのに対し、日能研では「62」、四谷大塚では「65」となっており、SAPIXと四谷大塚の偏差値の差はなんと偏差値で「9」もあるのです。
偏差値がそれぞれの塾で異なる理由は、僕の憶測ではおそらく2つあります。
第1に、各塾の母集団(入塾した生徒の総体)の学力レベルに差があるだろうということです。
一般的にSAPIXには学力レベルの一番高い子たちが通い、日能研や四谷大塚はその次の学力レベルの子たちが通っていると言われています。
なので、SAPIXでは塾内テストの偏差値が低くても、SAPIX外部生を含めた全国受験生の中での偏差値はもっと高くなると想定されるので、SAPIX偏差値が「56」でも十分に早稲田大学高等学院中等部に合格できる水準ということになるのだろうと思われます。
第2に、過去の塾内テストの生徒の偏差値と合格した学校を照らし合わせて、各学校が独自に偏差値を決めているのだろうということです。
つまり、その年の中学受験生という全国の母集団(受験生全体)の統一試験のような生データはそもそも存在しないので、その塾の過去の生徒の塾内偏差値データと合格実績を照合して、塾内の偏差値フレームワーク(枠組み)の中に各学校をプロットしているのだろうと思われるのです。
したがって、偏差値を目安に受験に臨むのは一般的だし結構なことですが、その偏差値はそれぞれの塾の運営母体ごとに、ある程度恣意的に出されたものであるということを認識しておいたほうが良さそうです。
世の中の多くの事象を説明できてしまう“正規分布”の魔力
ここでは、それらのサイトを参照・引用させていただく形で、文系脳の皆様にもご理解いただけるように文系オジさんの僕が難しい数式を登場させずにご説明いたします。
正規分布とは
まずは、統計学の世界では基本中の基本となる正規分布についてです。
＜図表1＞
正規分布の典型的な形正規分布とは統計・統計学を理解する上で一番大切な確率分布です。その名前（正規分布 normal distribution）からもわかる通り、”normal”な、「ありふれた」「通常の」確率分布です。名前の所以は、自然界や人間の行動・性質など様々な現象に対して、よく当てはまるところから来ています。そして、そのグラフは、下図のように左右対称な曲線になります。
引用元: AVILEN AI Trend “正規分布の分かりやすいまとめ”
“曲線の意味がそもそもよく分からない…”という方もいらっしゃると思うのですが、この曲線は以下のように“度数分布表(縦棒グラフ)を滑らかに線で表したもの”とご理解ください。
＜図表2＞
度数分布表を滑らかにしたベルの形の曲線
(ベルカーブ)
引用元: Hatsudy：総合学習サイト “統計での正規分布：連続型確率分布での標準正規分布の確率”
この曲線はベルカーブと呼ばれますが、“ベル”とはリンリン鳴らすジングルベルの“ベル”のことです。
ベル型の曲線が“ベルカーブ”
＜図表1＞の説明で「自然界や人間の行動・性質など様々な現象」に「よく当てはまる」とありましたが、会社での正規分布の事象を挙げるなら、《営業成績》《業務パフォーマンス》《会社の対する忠誠心の度合い》《有給休暇取得日数》、《工場で作る製品の品質》、《仕入商品の検品結果》などが挙げられ、もしかしたら《お給料》もそうかもしれません。
社会人になると「2・8の法則」あるいは「2・6・2の法則」という言葉を皆さんも聞いたことがあるかと思いますが、例えば「上位2割のモチベーションの高い社員が業務を回して会社を支えている」だとか、「会社の業績に貢献しているのは上位２割の社員、真ん中の6割は中間大衆(どちらかというとお荷物)、末端の2割は働いているフリをしている完全ぶら下がり状態のフリーライダー」というように言われます。この“法則”も、基本的には正規分布のベルカーブを元にした経験則と言えます。
学校での正規分布の事象を挙げるなら、クラス全員の《身長》《体重》《100m走のタイム》などですが、学校における正規分布の最たる例が《テストの成績》です。
例えば、東京の私立中学トップである開成中学の2023年の四谷大塚の偏差値は「71」です。ということは、開成中学に合格した生徒は入学時点で全員が偏差値71であると想定されるのですが、入学してからの学内テストの点数は必ず正規分布の形でバラつき、開成中学という新たな母集団の中では偏差値70の子もいれば、偏差値40の子もいるということになるのです。
このように、世の中の多くの事象が正規分布に従ってバラつき、別の会社や学校(別の母集団)であったとしても、同じように正規分布の形で分布するのです。
ということで、文系脳で正規分布の性質を理解するなら、次の3つだけ抑えておけば大丈夫です。
正規分布の代表的な性質
- 平均値の観測データが生じる確率が最も大きい(グラフ中央の山が高い)
- 平均値を中心にして左右対称である(綺麗な線対称)
- 平均値から離れるほどデータが生じる確率は小さくなる(両端に近づくほど低い値となる)
標準偏差とは
＜図3＞ように、平均値に多くのデータが集中しているため中央の山が高いベルカーブもあれば、その逆に、データのバラつきが大きくて両端の裾野の幅が左右に長いベルカーブもあります。
＜図表3＞
形が違うベルカーブ
引用元: 統計LIFE “正規分布とは何か 基本的な性質や身近な例とともに解説”
ベルカーブの形が違うということは、つまり“その母集団のデータのバラつき方が違う”ということであり、それぞれのデータ群(母集団)の性質が異なることを意味します。
それぞれのデータ群(母集団)のバラつきの度合いを表す値として、“標準偏差(σ=シグマ)”という概念があります。
標準偏差はちょっと複雑な計算式で算出されるためここでは割愛しますが、その値はデータ群(母集団)によって異なります。
＜図表4＞ように、データのバラつきが大きければ大きいほど(山がなだらかなほど)標準偏差の値は大きくなり、データのバラつきが小さければ小さいほど(中央の山が高いほど)標準偏差の値は小さくなります。
＜図表4＞
標準偏差の大小の違い
引用元: アガルートアカデミー “統計学でよく聞く「分散」と「標準偏差」”
いまいちピンときてない方も多いと思うのですが、どんなデータ群(母集団)でも十分なサンプル数があれば、エクセルで簡単に標準偏差(σ)の値を求めることができます。
そしてこの標準偏差は、実はものすごく有用なデータを提供してくれるとても有難い存在なのです。
つまり、標準偏差を用いればどんな形のベルカーブでも同じ尺度でデータのバラつきの範囲を把握することができ、“平均値(中央)からどれくらい離れた範囲の中に何%のデータが含まれるのか？”という共通の情報を私たちに与えてくれるのです。
＜図表5＞をご覧ください。
＜図表5＞
正規分布と標準偏差(σ=シグマ)
引用元: AVILEN AI Trend “標準偏差の意味と求め方”
標準偏差は英語では「σ(シグマ)」と呼ばれ、データ群(母集団)のバラつきの範囲を把握する時に、1σ(1シグマ)、2σ(2シグマ)、3σ(3シグマ)などの形で頻繁に使われます。
大学院のMBAコースでは、製造業での良品製造率6σを目指して高品質な製品を安定的に供給し顧客満足を高めることで売上の最大化を図る「シックスシグマ(6σ)」というコンセプトや、製品市場が市場に普及する過程を説明する「イノベーター理論」や「キャズム理論」など、正規分布を前提とした概念として学びました。(もはやどれも古典だなw)
標準偏差の目線からデータ群を眺めると、平均値(中央)から1σ(標準偏差1)の範囲の中にはデータの68.3%が入り、2σ(標準偏差2)の範囲の中にはデータ群の95.4%が入り、3σ(標準偏差3)の範囲の中には99.7%のデータが必ず入ることが分かります。
| 標準偏差の幅 | 範囲内に入る確率 |
|---|---|
| ±1σ 平均値プラスマイナス標準偏差1 |
68.3% |
| ±2σ 平均値プラスマイナス標準偏差2 |
95.4% |
| ±3σ 平均値プラスマイナス標準偏差3 |
99.7% |
上記のとおり、どんなバラつきの形の正規分布でも、上記の標準偏差の範囲内にこの割合のデータが必ず入るんです。とっても不思議ですよね。これが統計学の面白いところなのです。
そして、この標準偏差こそが偏差値計算の基本となっているのです。
偏差値の算出方法のおさらい
“偏差値”は日本独特の学力を把握するための指標で、受験者の中で自分の相対的な位置を示します。
受験者全員の点数のバラつきが正規分布に従うことを前提とし、点数の平均値(平均点)を偏差値50、標準偏差「±1」の値が偏差値では「±10」となるよう目盛りが設定されています。
平均点と同じ点数なら偏差値は50であり、+1σ(標準偏差+1)の位置にいれば偏差値は「50+10」となるので「偏差値60」となり、+2σ(標準偏差+2)の位置にいれば偏差値は「50+20」となるので「偏差値70」となります。
“難しい計算式は一切抜き”と冒頭で申し上げましたが、偏差値の計算方法だけ紹介させていただきます。
＜図表6＞
偏差値の数式
引用元: AVILEN AI Trend “偏差値の意味、求め方、性質などのまとめ”
標準偏差は生データがないと算出することができませんので、偏差値も基本的には生データを元に算出するものとなります。
＜図表5＞の正規分布・標準偏差の図に偏差値を重ね合わせたものが、次の＜図表7＞です。
＜図表7＞
正規分布と偏差値の対応関係
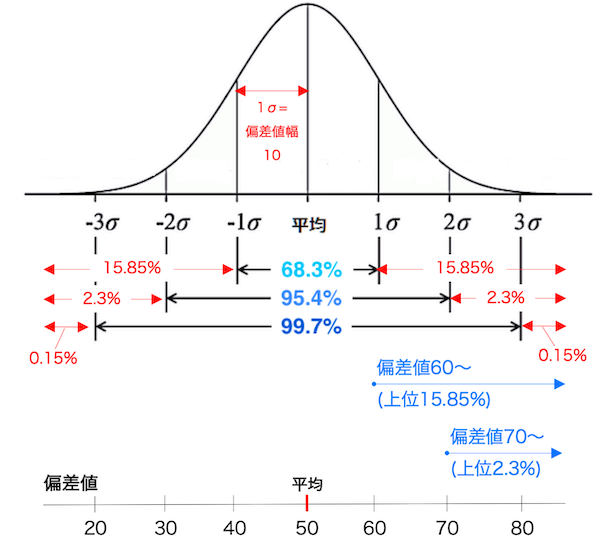ここで分かることは、“偏差値60や偏差値70は、母集団の中でいったいどの位置にいるのか？”ということです。
整理すると、以下のようになります。
| 偏差値 | 標準偏差 | 母集団の中の位置 |
|---|---|---|
| 80〜 | +3σ | 上位0.15% |
| 70〜 | +2σ | 上位2.3% |
| 60〜 | +1σ | 上位15.85% |
| 50〜 | — | 上位50% |
こう見てみると、偏差値70を叩き出せるのは上位2.3%の生徒となり、1学年100人のインターナショナルスクールなら、わずか2人ということになります。ましてや偏差値80ともなると天然記念物級です(笑)
この正規分布と標準偏差の理屈を押さえると、偏差値の構造がだいぶ見えてきたのではないかと思います。
A-Levelの偏差値を出すために参照した重要情報
次に、Aレベルの偏差値を出すために有益な某国式インターの高校卒業資格とそのスコアについてご説明いたします。
某国式インターの高校卒業資格とスコア
マレーシアには、いくつもの国のカリキュラムのインターナショナルスクールが存在します。
ここで参考にするのは…
